Solving the Pentomino Puzzle: Constraint Solving with AI and Replit

Written By Saqiba Najam

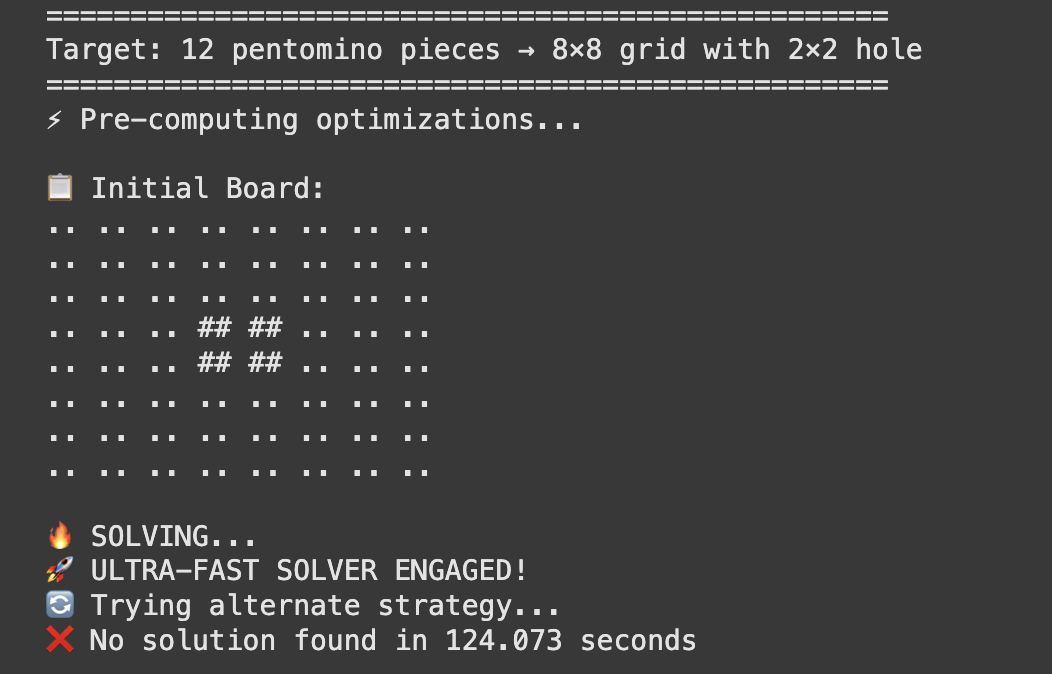
I recently took on a challenging variation of the classic Pentomino Puzzle. The goal was to fit all 12 unique pentomino pieces into an 8×8 grid, leaving a fixed 2×2 hole in the center. Each piece had to be used exactly once, with full rotation and reflection allowed. No overlaps or gaps.

This is a well-known constraint satisfaction problem with a huge search space (around 12! × 8¹² possibilities). Here's how I approached it:

Thought Process:

Tried multiple algorithms.. but failed.

  • Started with recursive backtracking, but quickly saw the need for smarter pruning.

  • Applied a Most Constrained Variable (MCV) heuristic to prioritize tighter board regions.

  • Added connected region checks to rule out impossible paths early.

  • Precomputed all rotations and reflections for efficiency.

  • Introduced early termination rules based on remaining pieces and board layout.

Tools and Collaboration:

  • Built and tested the solver using Replit, which made rapid iteration easy.

  • Used both Claude and GPT-4 for idea generation, edge case handling, and refining logic.

Result:

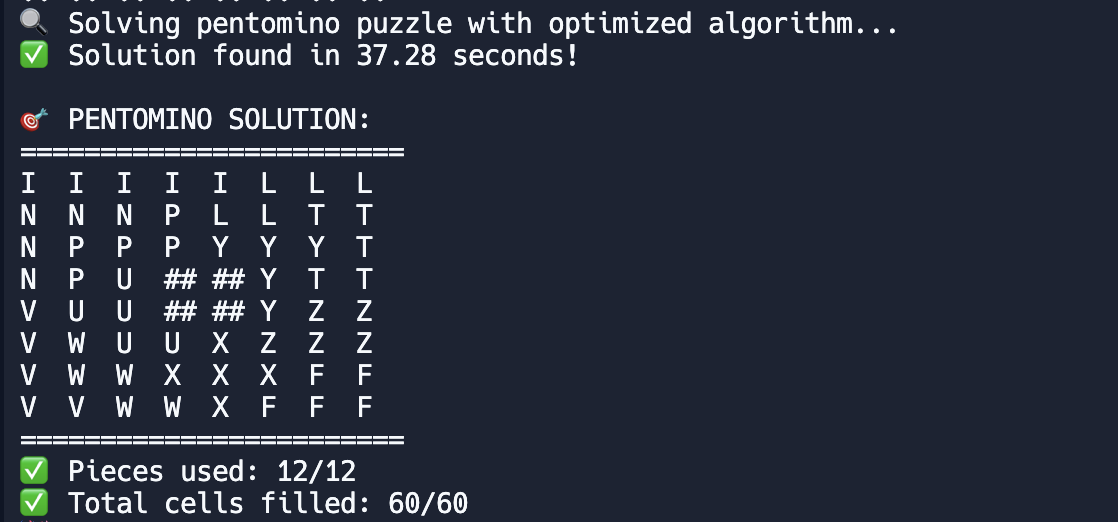
The solver found a valid solution in about 47 seconds. A great reminder that combining classic algorithm design with modern AI tools can make even massive search problems solvable.

Pentomino Solution

Console view

Saqiba Najam
Next

On Talent